A Monte Carlo Example
Consider the following active filter circuit.
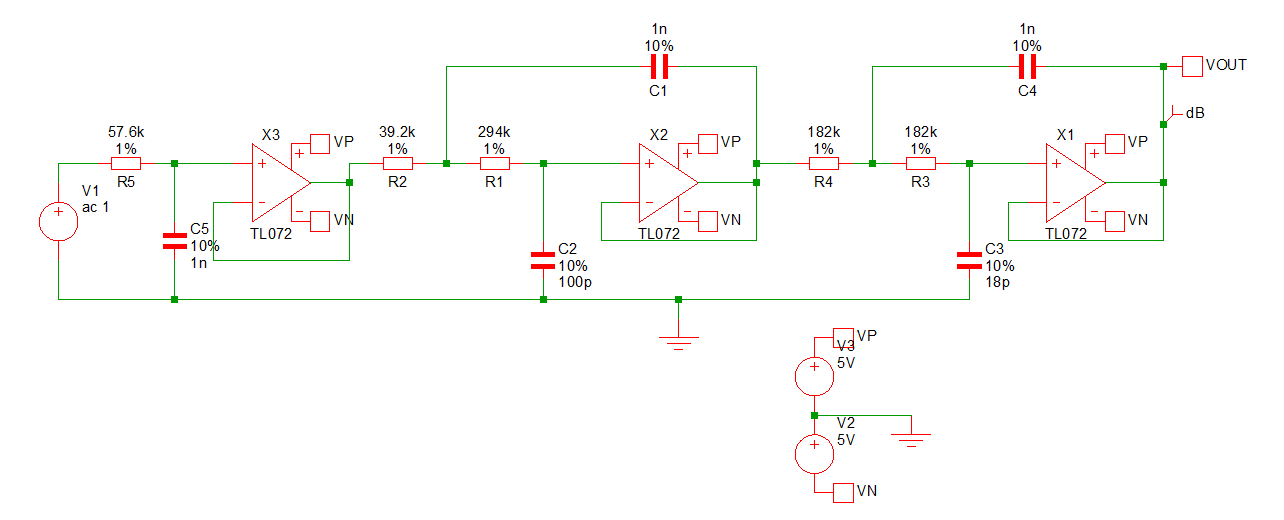
This circuit can be found in EXAMPLES/MonteCarlo/cheb2.sxsch
The circuit is a 5th order low-pass 7kHz Chebyshev filter with a 0.23dB passband ripple specification. Its nominal response is:
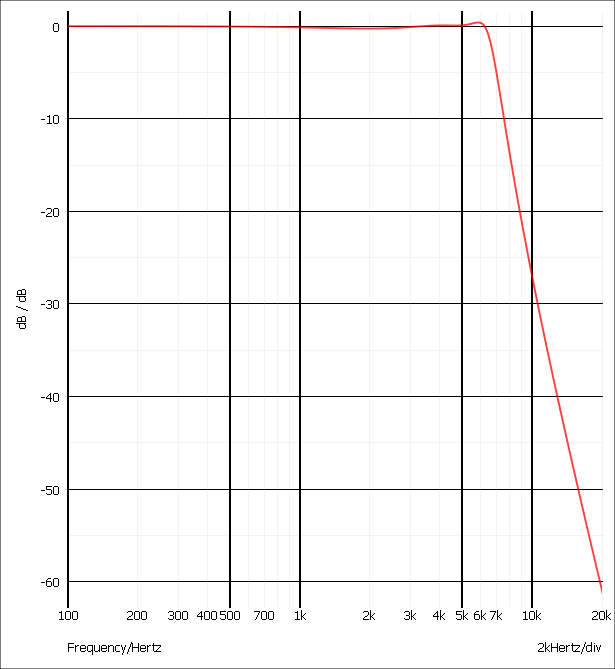
This circuit is to be used in an application that requires the gain of the amplifier to remain within 3dB of the dc value from 0 to 6kHz. A 0.23dB ripple specification therefore seems a reasonable choice. Clearly though the tolerance of the capacitors and resistors may upset this. To investigate, a Monte Carlo analysis mat be performed. The standard part tolerances are 10% for capacitors and 1% for resistors. With the example circuit the tolerances are already applied but the procedure for doing this is as follows:
- Select menu item
- Enter 1%. (The % is recognised)
- Select menu item
- Enter 10%.
- Select menu
- Note in the section Monte Carlo and Multi-step Analysis the Enable multi-step box is checked.
- Press the Define... button.
- Note that in the Sweep Mode section, Monte Carlo is selected and in the Step Parameters section. Number of steps has been set to 100.
Start the analysis in the usual way. It should take less than 1 second to run.
The analysis will be repeated 100 times. Now plot the output of the filter in the usual way (
). The result is the following:
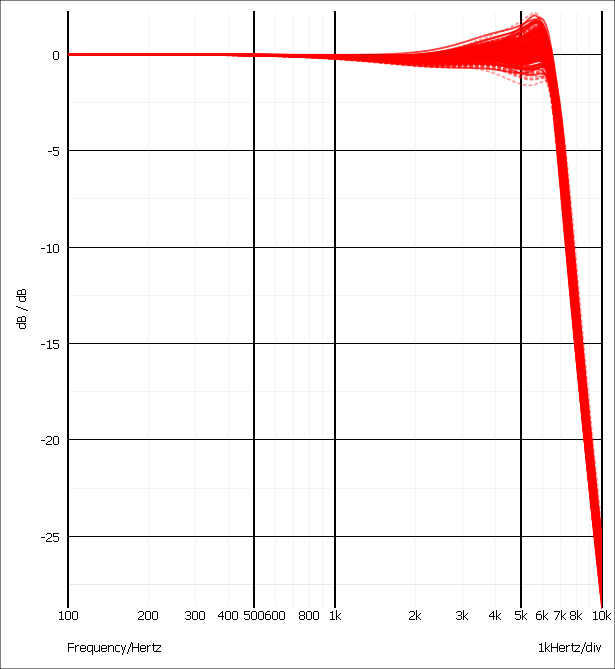
As can be seen, the specification is generally met. In the next section Sensitivity/Worst-case Example we will perform a worst-case analysis on the circuit which will show that there are extreme combinations of values that do not meet the spec.
- Random variation of device model parameters.
- Support for matched devices.
- Log file creation
- Seed selection to allow repeated runs with same randomly applied values.
| ◄ Monte Carlo, Sensitivity and Worst-case Analyses | Sensitivity/Worst-case Example ▶ |