Multipliers
Multiplication and division of two or more arbitrary time-varying signals is not a piecewise linear (PWL) operation. Since the SIMPLIS simulation engine uses PWL mathematics, multiplication and division are typically implemented at the circuit level, although SIMPLIS does have built-in Non-Linear Block (NLB) Multiplier/Dividers. This topic briefly describes the three multiplication methods in SIMPLIS.
In this topic:
Multiplication of a Time-Varying Signal by a Constant
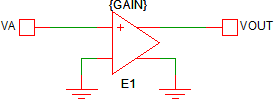
This is the one case where you actually don't need a multiplier at all. Multiplication of a time-varying signal by a constant value is a simple gain operation and can be implemented with a voltage-controlled voltage source. The following circuit implements the equation ???MATH???V_{OUT} = GAIN \times V_A???MATH???.
Multiplication Methods
There are three common ways to multiply or divide time-varying signals in SIMPLIS:
- Piecewise Linear Multipliers - PWL Multipliers
- Pulse Width Modulated Multipliers - PWM Multipliers
- Built-in Non-Linear Block Multipliers - Non-Linear Block (NLB) Multiplier/Dividers
As each method has design tradeoffs in bandwidth and accuracy, knowledge of the appication is required before choosing a method. In the next section each multiplication method is described along with it's advantages and disadvantages.
PWL Multiplication
The PWL multiplication method exploits the fact that the multiplication of two time-varying signals, ???MATH???V_A???MATH??? and ???MATH???V_B???MATH??? can be represented in a log-anti-log format:
\[ V_A \times V_B = 10^{\left( log\left( V_A \right) + log \left( V_B \right) \right)}\]
This method uses PWL resistors to create the ???MATH???log\left( V_A \right)???MATH??? and $log\left( V_B \right)$ signals, these signals are then added with a Summer and a final anti-log PWL resistor is used to generate the output voltage.
Advantages:
- Infinite bandwidth. A very fast moving signal applied to the input will appear at the output without delay.
- Compatible with the POP and AC analyses
Disadvantages:
- Poor accuracy around portions of the input range. This inaccuracy is due to the fact that the log and anti-log portions of the multiplier are PWL and not continuous.
PWM Multiplication
The PWM multiplication method uses an ideal buck converter and a filter to multiply two time-varying signals. The buck converter transfer function is:
\[ V_{OUT} = duty cycle \times V_{IN}\]
The two input signals ???MATH???V_A???MATH??? and ???MATH???V_B???MATH??? are mapped into the buck converter's inputs ???MATH???duty cycle???MATH??? and ???MATH???V_{IN}???MATH???. Because the duty cycle of a buck converter can only take on values between 0 and 1.0 inclusively, the maximum amplitude of the input signal which is mapped to the ???MATH???duty cycle???MATH??? input needs to be known. The signal being mapped to the duty cycle input is first divided by it's known maximum voltage, which is a constant value, before being input to the multiplier. In the following expression, the ???MATH???V_A???MATH??? input is mapped to the ???MATH???duty cycle???MATH??? input and the ???MATH???V_A???MATH??? input has a known maximum voltage of ???MATH???V_{A0}???MATH???, which is a constant.
\[ V_{OUT} = V_{A0} \times \frac{V_A}{V_{A0}} \times V_{B} = V_A \times V_B \]
Finally, an output filter is required to remove the switching ripple. The filter type, number of poles, and pole location are up to the user.
Advantages:
- High precision at low frequencies. The idealized buck converter which uses the Switched Voltage-Controlled Voltage Source has no losses and implements the theoretical buck transfer function of ???MATH???V_{OUT} = duty cycle \times V_{IN}???MATH??? exactly.
- Compatible with the POP and AC analyses
Disadvantages:
- Poor high frequency performance. The output of a PWM multiplier is heavily filtered to remove the switching ripple, which leads to significant phase shift at low frequencies. This phase shift limits the multiplier to applications such as PFC converters where the maximum bandwidth required is in the kHz range.
NLB Multiplication
SIMPLIS comes with built-in Non-Linear Multiplier/Divider Blocks. These blocks offer more flexibility than the PWL and PWM multiplication methods, but at a cost: the modeling methods behind the NLB blocks are not compatible with the POP and AC analyses.
Advantages:
- Wide bandwidth controlled by a low pass filter built into each block.
- Many different multiply/divide operations are available.
Disadvantages:
- Not compatible with the POP and AC analyses.
- Possibly slow simulations at certain input voltages.
- These are the least accurate blocks in SIMPLIS.